Contents

1 Vectors

1-10 OTHER DIFFERENTIAL OPERATIONS

$$\triangledown\cdot\vec{A}=\frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z}\tag{1-42}$$ This scalar product is called the divergence of A and is often written div A. Using (1-27) and (1-41), we obtain $$\triangledown \times \vec A = \left ( \frac {\partial A_z}{\partial y} - \frac {\partial A_y}{\partial z} \right )\hat x +\left ( \frac {\partial A_x}{\partial z} - \frac {\partial A_z}{\partial x} \right )\hat y +\left ( \frac {\partial A_y}{\partial x} - \frac {\partial A_x}{\partial y} \right )\hat z \tag{1-43}$$ This vector porduct is called the curl of A and is often written curl A it can also be conveniently written as a determinant as in (1-28): $$\triangledown \times \vec A = \left | \begin{matrix} \hat x & \hat y & \hat z\\ \frac {\partial}{\partial x} & \frac {\partial}{\partial y} & \frac {\partial}{\partial z}\\ A_x & A_y & A_z \end{matrix} \right | \tag{1-44}$$

1-17 SPHERICAL COORDINATES

$$\hat r = sin \theta cos \phi \hat x + sin \theta sin \phi \hat y + cos \theta \hat z\tag{1-93}$$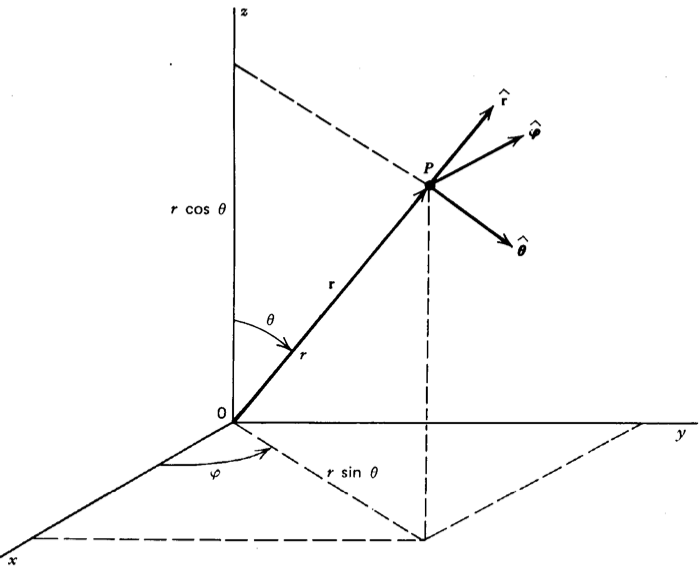

2 Coulomb's law

2-2 Coulom's Law

$$\epsilon_0=8.85\times10^{-12} (coulomb)^2/newton-(meter)^2$$
$$=8.85\times10^{-12} farad/meter$$

3 The electric field

3-3 FIELD OF A UNIFORM INFINITE PLANE SHEET

figure 3-3 Calculaion of the field due to uniform infinite plane sheet.
$$\vec{E}=\frac{\sigma}{2\epsilon_0}\left(\frac{z}{|z|}\right) \hat{z}\tag{3-13}$$

4 GAUSS’ LAW

4-1 DERIVATION OF GAUSS’ LAW

We want to show that $$\oint_S \vec E \cdot d\vec a= \frac{1}{\epsilon_0} \sum_{inside} q_i = \frac{Q_{in}}{\epsilon_0}\tag{4-1}$$ $$Q_{in}=\int_V \rho \; d\tau$$ $$\triangledown\cdot\vec{E}=\frac{\rho}{\epsilon_0}\tag{4-10}$$

4-2 SOME APPLICATIONS OF GAUSS’ LAW

Example

Uniform infinite line charge. We can write it as the sum of integrals over the curved surface, and the upper and lower faces (which we designate as c, u, and l).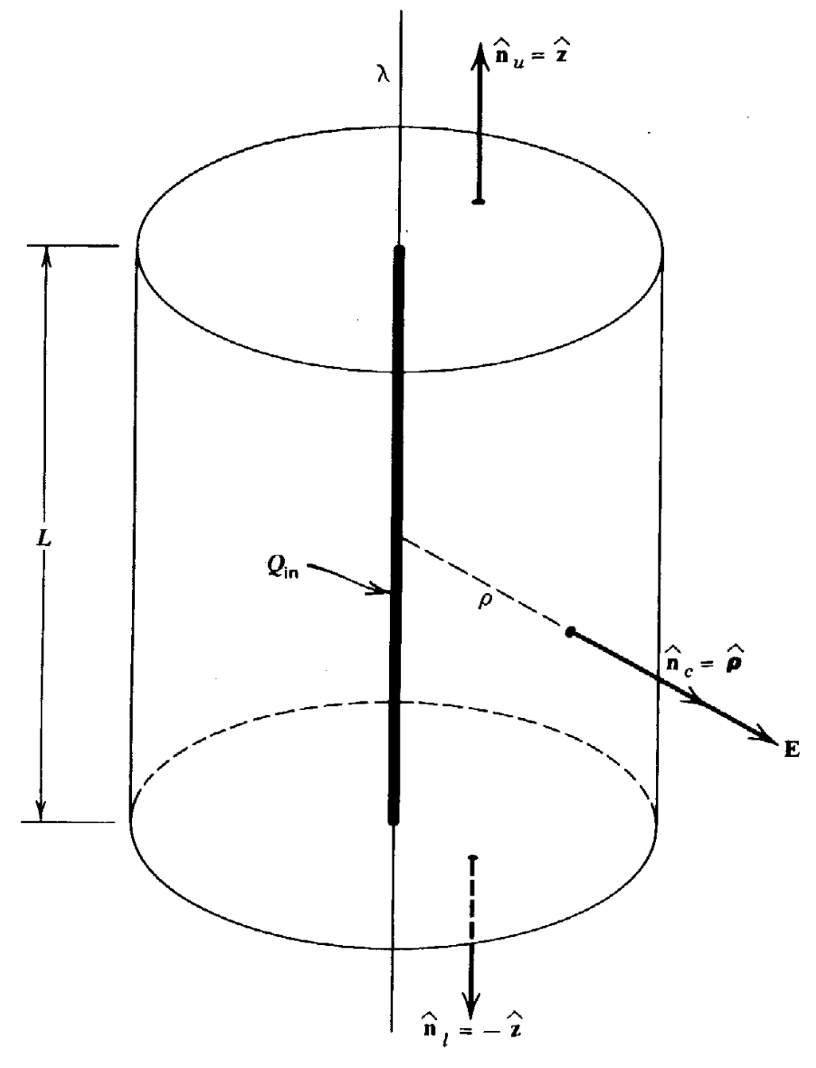 Figure 4-3. Calculation of the field of a uniform infinite line charge.
this case, $$\oint_S \vec E \cdot d\vec a= \int_c E_\rho (\rho) \hat \rho \cdot \hat n_c da + \int_u E_\rho (\rho) \hat \rho \cdot \hat n_u da + \int_l E_\rho (\rho) \hat \rho \cdot \hat n_l da $$

10 ELECTROSTATICS IN THE PRESENCE OF MATTER

10-5 THE D FIELD

$$\vec{D}=\epsilon_0 \vec{E}+\vec{P}\tag{10-40}$$ $$\triangledown\cdot\vec{D}=\rho_f\tag{10-41}$$ Gauss’ law forD is easily found from (10-41) and (1-59) to be $$\oint_S \vec D \cdot d\vec a = \int_V \rho_f \; d\tau = Q_{f,in} \tag{10-43}$$ where Q_{f,in} is the net free charge contained within the volume V surrounded by the closed surface S.

20 MAGNETISM IN THE PRESENCE OF MATTER

20-4 THE H FIELD

$$\triangledown \times \vec{H}=\vec {J} _f \tag{20-29}$$ The vector H is called the magnetic field or sometimes the H field.
The integral form of Ampére’s law for H can be found by using (20-29), (1-67), and (12-6); the result is that $$\oint _C \vec{H} \cdot d \vec{s} = \int _S \vec {J} _f \cdot d \vec{a} = I_{f,enc} \tag{20-32}$$

24 PLANE WAVES

24-2 PLANE WAVES IN A NONCONDUCTING MEDIUM

The spatial period lamda is called the wavelength, $$|k|= \frac{2\pi}{\lambda} \; \omega = 2 \pi \nu = \frac{2\pi}{T} \tag{24-27}$$